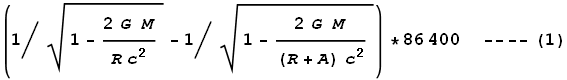Clocks on GPS satellites

from alternativephysics

Another strong piece of evidence supporting GR, and which affects our everyday lives, is the Global Positioning System (GPS). We are told that GPS satellites experience a net time dilation of 38,700ns (nanoseconds) a day: +45,900ns due to GR and -7,200ns due to SR. We discussed the SR aspects of this in an earlier chapter. Now let’s look at GR.

The satellites orbit at an approximate altitude of 20,200km. Using equation (3) in the chapter on General Relativity we can calculate the expected differences in time dilation at the Earth’s surface and at the satellite:

Where M is the mass of Earth, R is the radius, A is the altitude of the GPS, and 86400 is the number of seconds in a day. Substituting values of M=5.974x10²⁴, R=6.357x10⁶, and A=2.02x10⁷ we get:

Net dilation = 45850 ns.

And this closely matches the measured amount. Brilliant!